A single molecular formula can represent a number of molecular isomers. Each isomer is a local minimum on the energy surface created from the total energy as a function of the coordinates of all the nuclei. A stationary point is a geometry such that the derivative of the energy with respect to all displacements of the nuclei is zero. A local (energy) minimum is a stationary point where all such displacements lead to an increase in energy. The local minimum that is lowest is called the global minimum and corresponds to the most stable isomer. If there is one particular coordinate change that leads to a decrease in the total energy in both directions, the stationary point is a transition structure and the coordinate is the reaction coordinate. This process of determining stationary points is called geometry optimization.
The determination of molecular structure by geometry optimization became routine only after efficient methods for calculating the first derivatives of the energy with respect to all atomic coordinates became available. Evaluation of the related second derivatives allows the prediction of vibrational frequencies if harmonic motion is estimated. More importantly, it allows for the characterization of stationary points. The frequencies are related to the eigenvalues of the Hessian matrix, which contains second derivatives. If the eigenvalues are all positive, then the frequencies are all real and the stationary point is a local minimum. If one eigenvalue is negative (i.e., an imaginary frequency), then the stationary point is a transition structure. If more than one eigenvalue is negative, then the stationary point is a more complex one, and is usually of little interest. When one of these is found, it is necessary to move the search away from it if the experimenter is looking solely for local minima and transition structures.
The total energy is determined by approximate solutions of the time-dependent Schrödinger equation, usually with no relativistic terms included, and by making use of the Born–Oppenheimer approximation, which allows for the separation of electronic and nuclear motions, thereby simplifying the Schrödinger equation. This leads to the evaluation of the total energy as a sum of the electronic energy at fixed nuclei positions and the repulsion energy of the nuclei. A notable exception are certain approaches called direct quantum chemistry, which treat electrons and nuclei on a common footing. Density functional methods and semi-empirical methods are variants on the major theme. For very large systems, the relative total energies can be compared using molecular mechanics. The ways of determining the total energy to predict molecular structures are:
1. Ab Initio methods
The programs used in computational chemistry are based on many different quantum-chemical methods that solve the molecular Schrödinger equation associated with the molecular Hamiltonian. Methods that do not include any empirical or semi-empirical parameters in their equations – being derived directly from theoretical principles, with no inclusion of experimental data – are called ab initio methods. This does not imply that the solution is an exact one; they are all approximate quantum mechanical calculations. It means that a particular approximation is rigorously defined on first principles (quantum theory) and then solved within an error margin that is qualitatively known beforehand. If numerical iterative methods have to be employed, the aim is to iterate until full machine accuracy is obtained
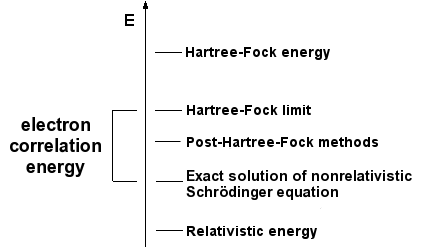
The simplest type of ab initio electronic structure calculation is the Hartree–Fock scheme, an extension of molecular orbital theory, in which the correlated electron–electron repulsion is not specifically taken into account; only its average effect is included in the calculation. As the basis set size is increased, the energy and wave function tend towards a limit called the Hartree–Fock limit. Many types of calculations (known as post-Hartree–Fock methods) begin with a Hartree–Fock calculation and subsequently correct for electron–electron repulsion, referred to also as electronic correlation. As these methods are pushed to the limit, they approach the exact solution of the non-relativistic Schrödinger equation. In order to obtain exact agreement with experiment, it is necessary to include relativistic and spin orbit terms, both of which are only really important for heavy atoms. In all of these approaches, in addition to the choice of method, it is necessary to choose a basis set. This is a set of functions, usually centered on the different atoms in the molecule, which are used to expand the molecular orbitals with the LCAO ansatz. Ab initio methods need to define a level of theory (the method) and a basis set.
The Hartree–Fock wave function is a single configuration or determinant. In some cases, particularly for bond breaking processes, this is quite inadequate, and several configurations need to be used. Here, the coefficients of the configurations and the coefficients of the basis functions are optimized together.
The total molecular energy can be evaluated as a function of the molecular geometry; in other words, the potential energy surface. Such a surface can be used for reaction dynamics. The stationary points of the surface lead to predictions of different isomers and the transition structures for conversion between isomers, but these can be determined without a full knowledge of the complete surface
2. Density functional methods
Density functional theory methods are often considered to be ab initio methods for determining the molecular electronic structure, even though many of the most common functionals use parameters derived from empirical data, or from more complex calculations. In DFT, the total energy is expressed in terms of the total one-electron density rather than the wave function. In this type of calculation, there is an approximate Hamiltonian and an approximate expression for the total electron density. DFT methods can be very accurate for little computational cost. Some methods combine the density functional exchange functional with the Hartree–Fock exchange term and are known as hybrid functional methods.
3. Semi-empirical and empirical methods
Semi-empirical quantum chemistry methods are based on the Hartree–Fock formalism, but make many approximations and obtain some parameters from empirical data. They are very important in computational chemistry for treating large molecules where the full Hartree–Fock method without the approximations is too expensive. The use of empirical parameters appears to allow some inclusion of correlation effects into the methods.
Semi-empirical methods follow what are often called empirical methods, where the two-electron part of the Hamiltonian is not explicitly included. For π-electron systems, this was the Hückel method proposed by Erich Hückel, and for all valence electron systems, the extended Hückel method proposed by Roald Hoffmann.
4. Molecular mechanics
In many cases, large molecular systems can be modeled successfully while avoiding quantum mechanical calculations entirely. Molecular mechanics simulations, for example, use a single classical expression for the energy of a compound, for instance the harmonic oscillator. All constants appearing in the equations must be obtained beforehand from experimental data or ab initio calculations.
The database of compounds used for parameterization is crucial to the success of molecular mechanics calculations. A force field parameterized against a specific class of molecules, for instance proteins, would be expected to only have any relevance when describing other molecules of the same class.
5. Methods for solids
Computational chemical methods can be applied to solid state physics problems. The electronic structure of a crystal is in general described by a band structure, which defines the energies of electron orbitals for each point in the Brillouin zone. Ab initio and semi-empirical calculations yield orbital energies; therefore, they can be applied to band structure calculations. Since it is time-consuming to calculate the energy for a molecule, it is even more time-consuming to calculate them for the entire list of points in the Brillouin zone.
Source: Wikipedia
No comments:
Post a Comment